Самопаркующаяся тачка в 500 строк кода

С помощью генетического алгоритма натренируем тачку парковаться самостоятельно.

Вкратце

В этой статье мы "научим" автомобиль выполнять самостоятельную парковку с помощью генетического алгоритма.

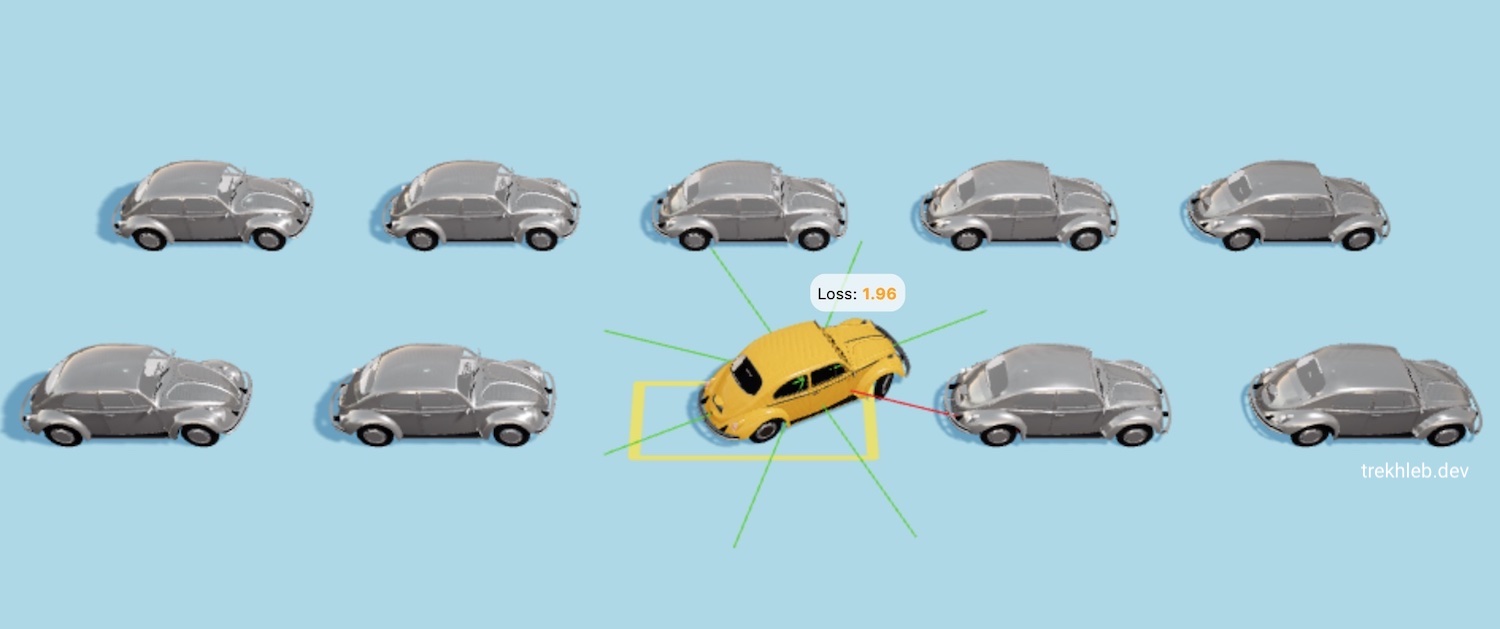
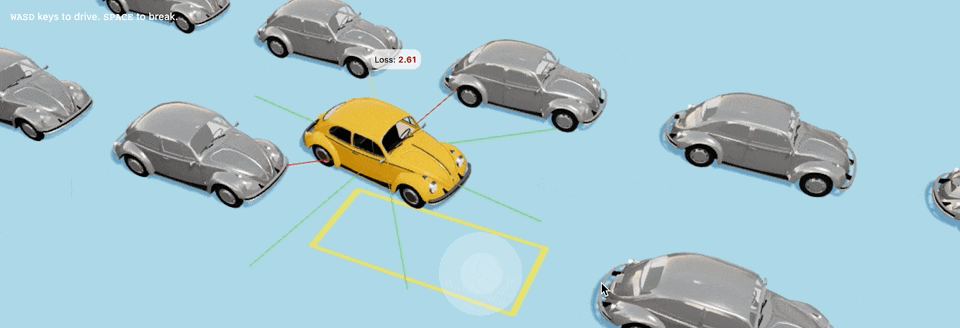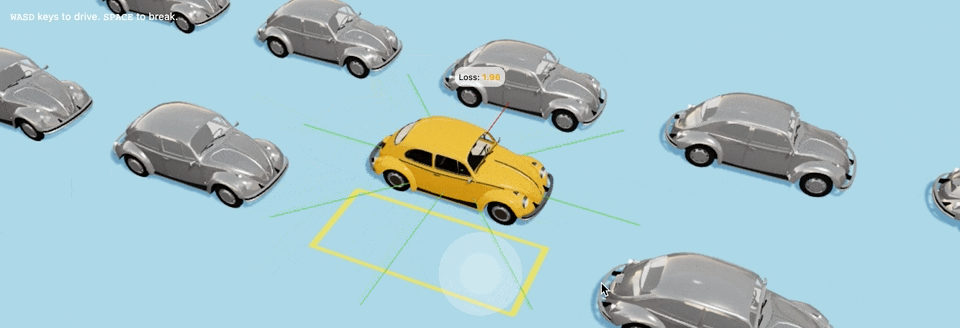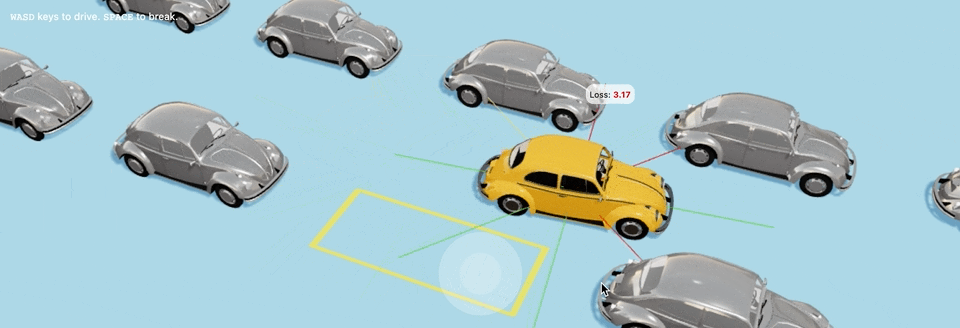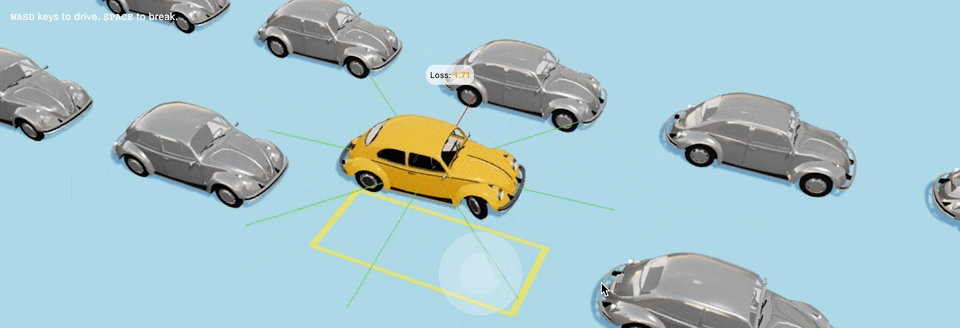
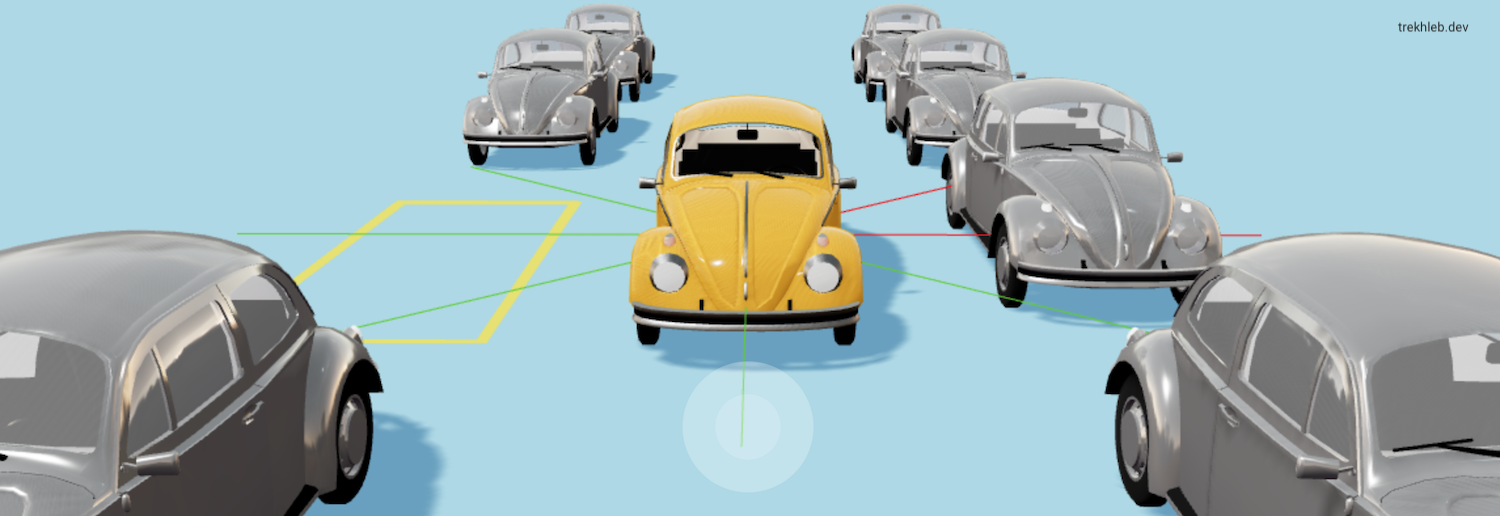
В 1-м поколении автомобили будут иметь случайный геном и будут вести себя хаотично, приблизительно вот так:

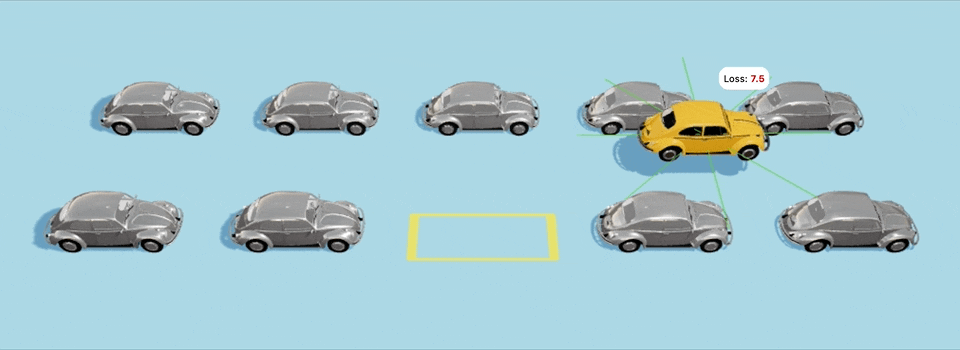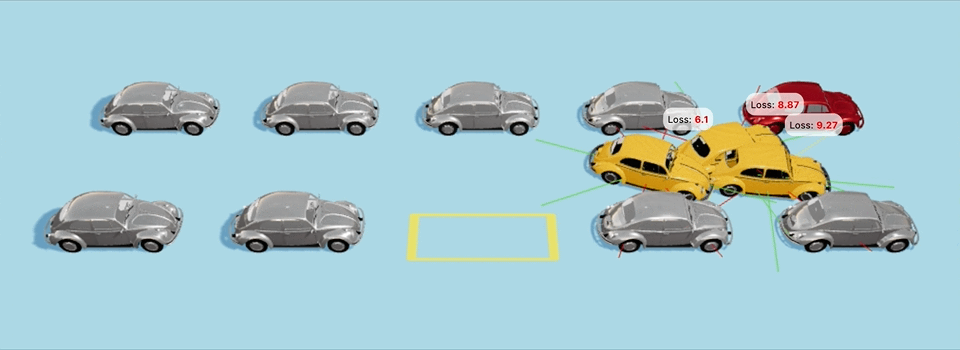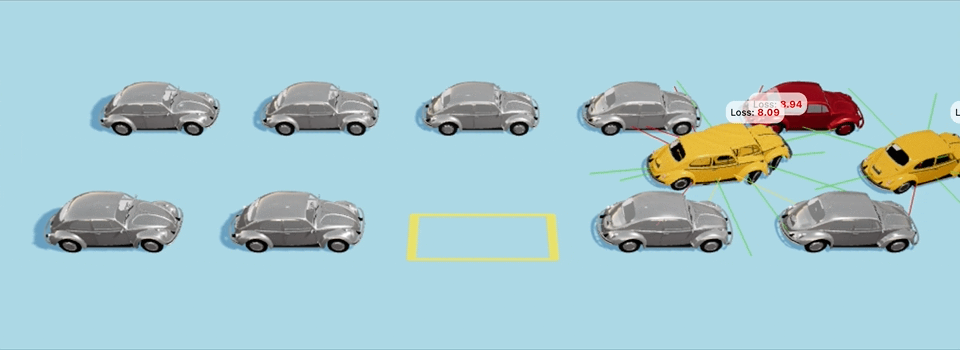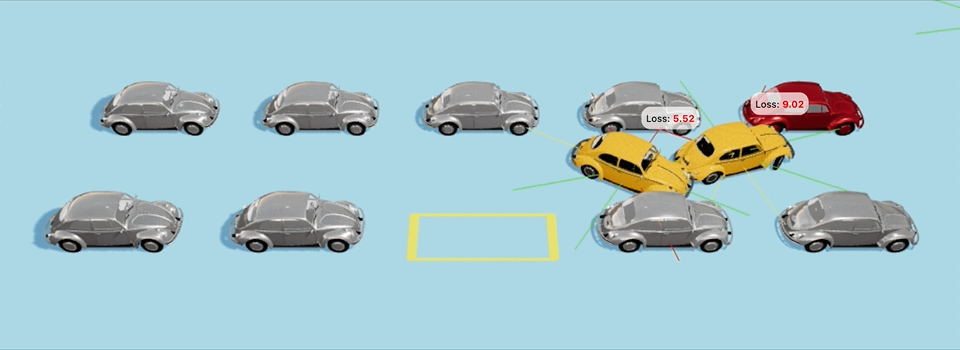
В ≈40-м поколении автомобили понемногу начнут учиться парковке и будут все ближе и ближе подбираться к парковочному месту,

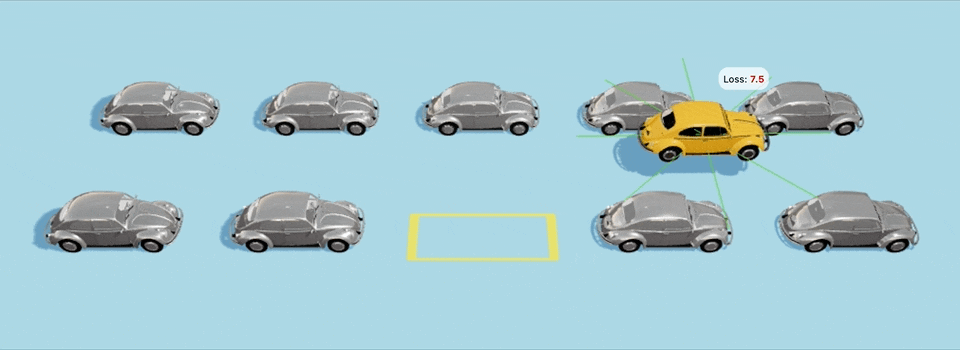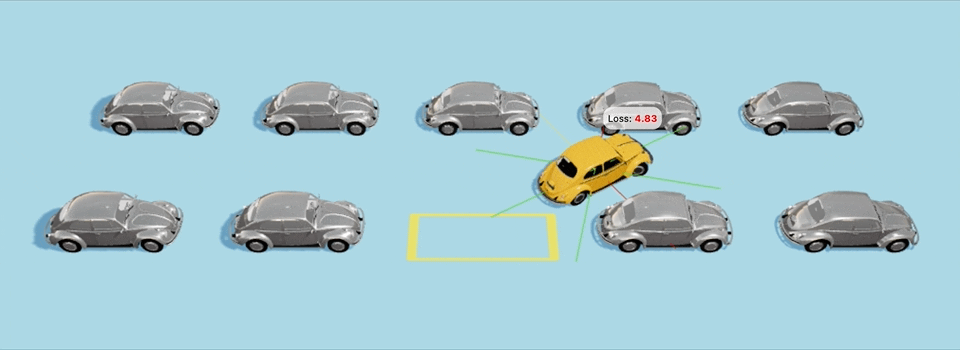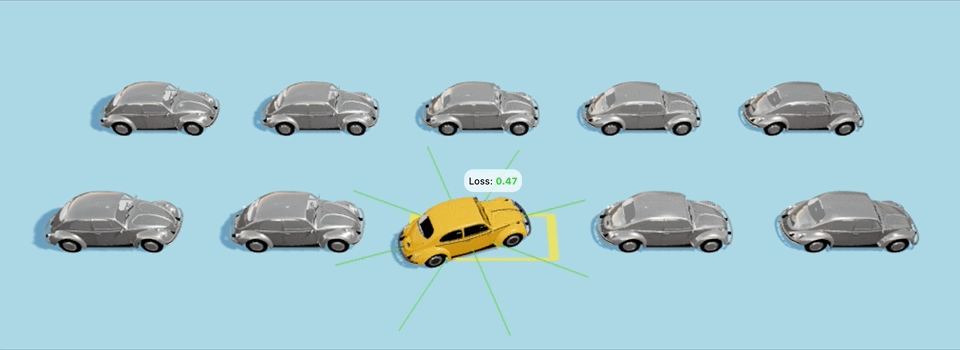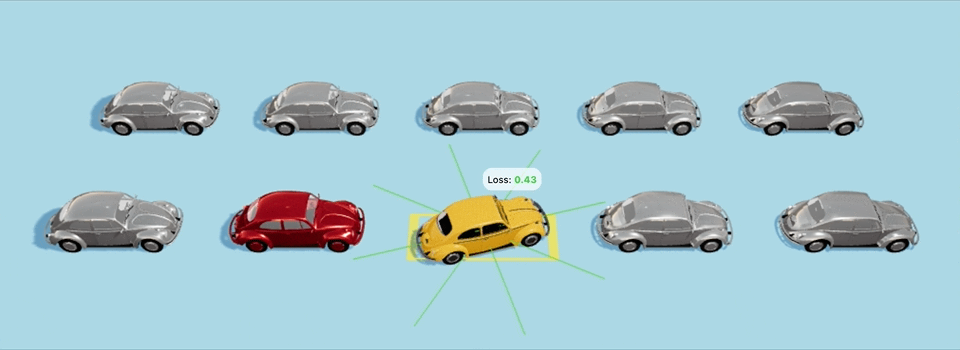
Еще один пример с более сложным стартовым положением:

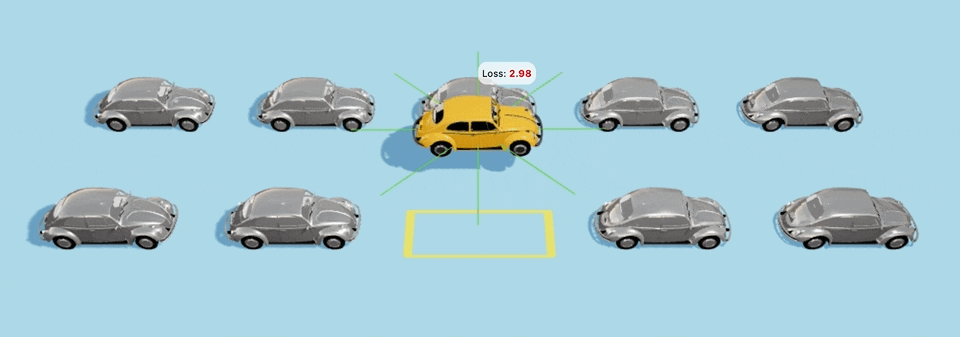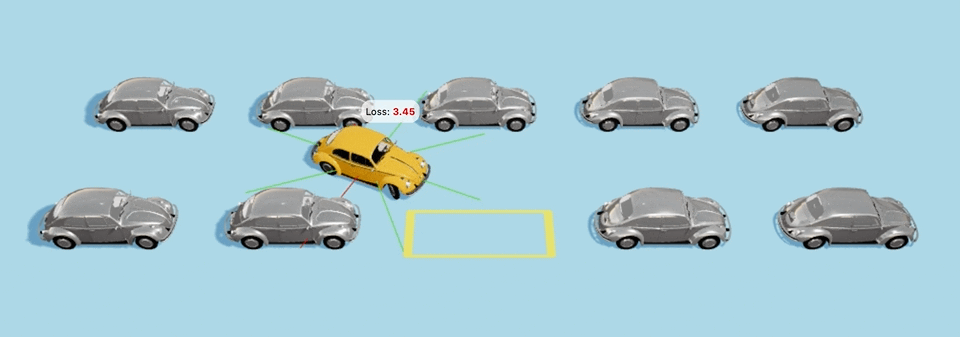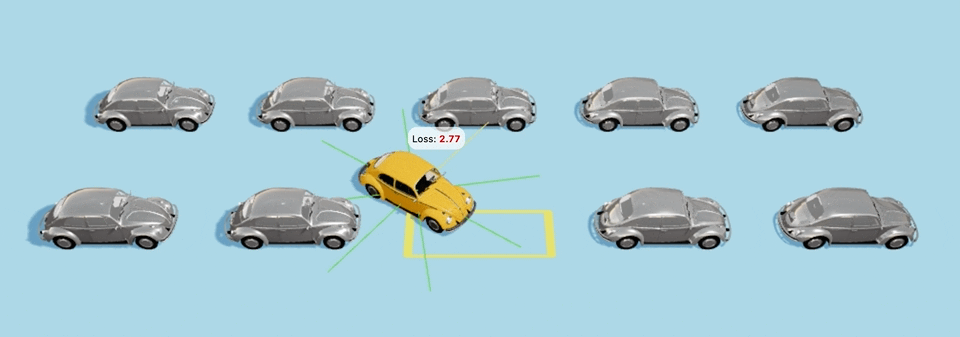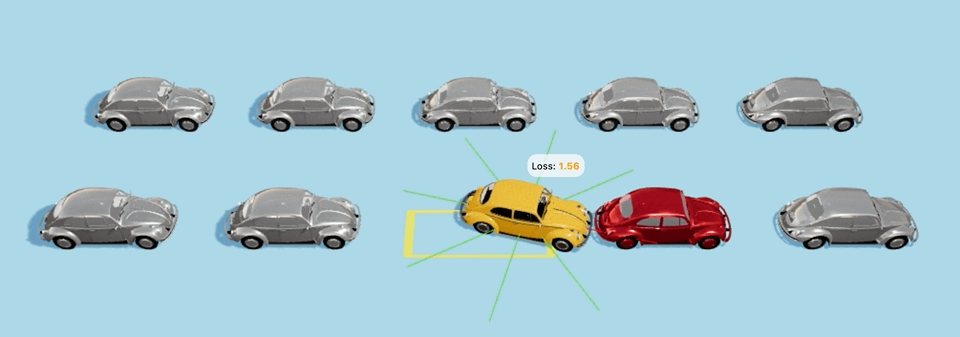
Да-да, машины врезаются в другие машины по пути, и неточно становятся на парковочное место, но для них это всего-лишь 40-е поколение с момента создания мира, так что будьте снисходительны и дайте машинам подрасти :D

Вы можете запустить 🚕 симулятор эволюции, чтобы увидеть эволюционный процесс прямо в браузере. Симулятор предоставляет следующие возможности:

• Вы можете начать тренировку машин с нуля и изменять параметры эволюции
• Вы можете увидеть как паркуются уже тренированные авто
• Вы также можете попробовать припарковать авто вручную

Генетический алгоритм для этого проекта будем реализовывать на TypeScript. В этой статье будет показан полный исходный код алгоритма, но вы также можете найти финальные примеры кода в репозитории симулятора.

Мы будем использовать генетический алгоритм для решения конкретной задачи обучения машин самостоятельной парковке. Однако эта статья затронет только основы алгоритма и ни в коем случае не будет являться полным руководством к нему.

С учетом вышесказанного, переходим к деталям...

План

Шаг за шагом мы сведем высокоуровневую задачу создания автомобиля способного парковаться автоматически к простой задаче нахождения оптимальной комбинации 180-и нулей и единиц (к нахождению оптимального генома).

Вот что мы собираемся сделать:

1. 💪🏻 Дадим машине мышцы (двигатель, руль), чтобы она могла двигаться в сторону парковочного места.
2. 👀 Дадим машине глаза (сенсоры), чтобы машина могла видеть препятствия вокруг.
3. 🧠 Дадим машине мозг, чтобы машина могла контролировать мышцы (движение) на основании того, что машина видит (препятствия через сенсоры). Мозг будет простой функцией movements = f(sensors).
4. 🧬 Разовьем мозг, чтобы он мог инициировать правильные движения на основании сигналов сенсоров. Здесь мы применим генетический алгоритм. Поколение за поколением функция мозга movements = f(sensors) будет учиться как приближать авто к парковочному месту.

Даем машине мышцы

Чтобы двигаться, машине нужны «мускулы». Дадим машине два типа мышц:

1. Мышца-двигатель - позволяет машине двигаться ↓ назад, ↑ вперед или ◎ оставаться на месте (нейтральная передача)
2. Мышца-руль - позволяет машине поворачивать ← влево, → вправо или ◎ ехать прямо.

С помощью этих двух мышц машина может выполнять следующие движения:

В нашем случае мышцы являются приемниками сигналов, поступающих от мозга каждые 100 мс (миллисекунд). В зависимости от значения сигнала мозга мышцы действуют по-разному. Мы рассмотрим «мозговую» часть ниже, а пока предположим, что наш мозг может посылать только 3 возможных сигнала каждой мышце: -1, 0 или +1.

type MuscleSignal = -1 | 0 | 1;

Например, мозг может послать сигнал со значением +1 в мышцу двигателя, и он начнет движение вперед. Сигнал -1 двигателю перемещает машину назад. В то же время, если мозг пошлет сигнал -1 в мышцу рулевого управления, он повернет машину влево и т.д.

Вот как в нашем случае значения сигналов мозга соотносятся с действиями мышц:

Вы можете использовать симулятор эволюции и попытаться припарковать машину вручную, чтобы увидеть, как работают мускулы машины. Каждый раз, когда вы нажимаете одну из клавиш клавиатуры WASD (или используете джойстик), вы посылаете эти -1, 0 или +1 сигналы двигателю и мышцам рулевого управления.

Даем машине глаза

Прежде чем наша машина научится самостоятельно парковаться, используя свои мышцы, она должна «видеть» окружающую среду. Дадим машине 8 глаз в виде датчиков расстояния:

• Каждый датчик может обнаруживать препятствие на расстоянии от 0 до 4 метров.
• Каждый датчик сообщает последние данные о препятствиях, которые он «видит» в «мозг» автомобиля каждые 100 мс.
• Когда датчик не видит никаких препятствий, он сообщает значение 0. Если же значение датчика небольшое, но не нулевое (например, 0.01 м), это будет означать, что препятствие близко.

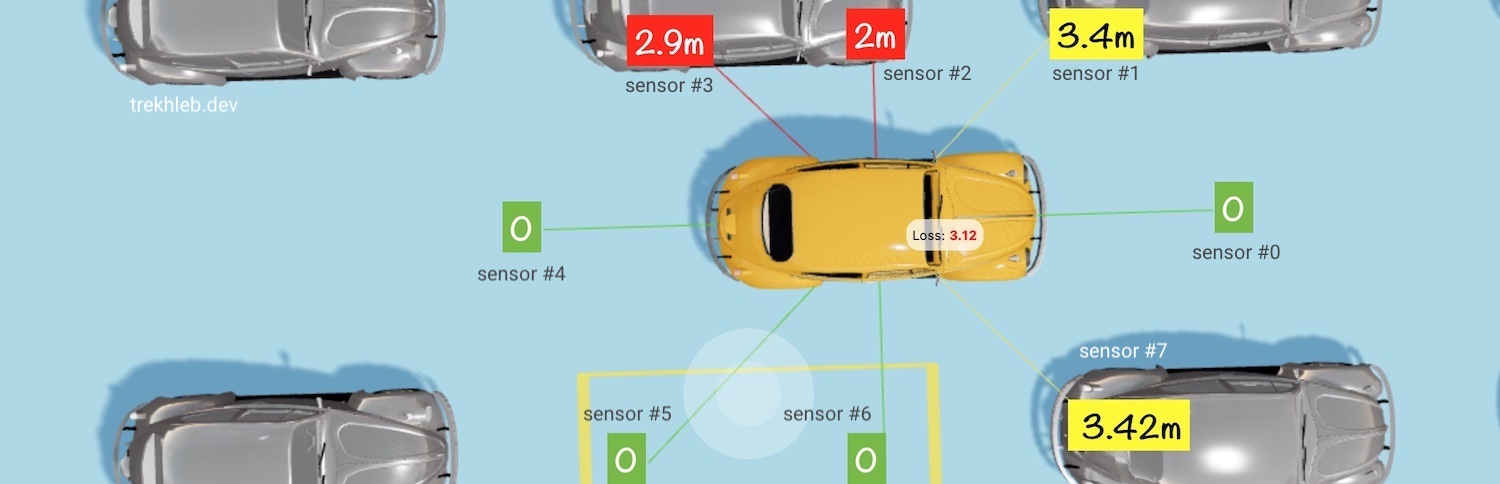
Вы можете воспользоваться симулятором эволюции и посмотреть, как меняется цвет каждого датчика в зависимости от того, насколько близко находится препятствие.

type Sensors = number[];

Даем машине мозг

На данный момент наша машина может «видеть» и «двигаться», но у нее нет «координатора», который преобразовывал бы сигналы от «глаз» в правильные движения «мускулов». Нам нужно дать машине «мозг».

Входящие сигналы мозга

В качестве входных данных от датчиков мозг будет получать 8 чисел с плавающей запятой каждые 100ms, каждое из которых находится в диапазоне [0...4]. Например, входящий сигнал от сенсоров может выглядеть так:

const sensors: Sensors = [s0, s1, s2, s3, s4, s5, s6, s7];
// i.e. 🧠 ← [0, 0.5, 4, 0.002, 0, 3.76, 0, 1.245]

Исходящие сигналы мозга

Каждые 100ms мозг должен выдавать на выходе два целых числа:

1. Одно число - сигнал для двигателя engineSignal
2. Другое число - сигнал для руля wheelSignal

Каждое число должно иметь тип MuscleSignal и может принимать одно из трех значений: -1, 0, или +1.

Мозговая функция

Учитывая упомянутые выше входящий и исходящий сигналы мозга, мы можем сказать, что мозг - это простая функция:

const { engineSignal, wheelSignal } = brainToMuscleSignal(
  brainFunction(sensors)
);
// i.e. { engineSignal: 0, wheelSignal: -1 } ← 🧠 ← [0, 0.5, 4, 0.002, 0, 3.76, 0, 1.245]

Где brainToMuscleSignal() - это функция, которая преобразует исходные сигналы мозга (любое число с плавающей запятой) в сигналы мышц (в одно из чисел -1, 0, или +1), чтобы мышцы могли это понять. Мы реализуем эту функцию-конвертер ниже.

Теперь главный вопрос, какой именно функцией должна быть brainFunction()?

Чтобы сделать машину "умнее", а ее движения - более сложными, мы могли бы использовать многослойный перцептрон. Название немного пугающее, но это простая нейронная сеть с базовой архитектурой (воспринимайте ее как большую формулу с множеством параметров/коэффициентов).

Я более детально коснулся темы многослойных перцептронов в проектах homemade-machine-learning, machine-learning-experiments и nano-neuron projects. Например, вы можете попросить эту простую нейронную сеть распознать нарисованные вами цифры.

Тем не менее, чтобы избежать введения совершенно новой концепции нейронных сетей в этой статье, мы воспользуемся гораздо более простым подходом и будем использовать два линейных многочлена с несколькими переменными (чтобы быть более точным, каждый многочлен будет иметь ровно 8 переменных, поскольку у нас есть 8 датчиков), которые будут выглядеть примерно так:

engineSignal = brainToMuscleSignal(
  (e0 * s0) + (e1 * s1) + ... + (e7 * s7) + e8 // <- brainFunction
)

wheelSignal = brainToMuscleSignal(
  (w0 * s0) + (w1 * s1) + ... + (w7 * s7) + w8 // <- brainFunction
)

Где:

• [s0, s1, ..., s7] - 8 переменных, которые являются 8 значениями датчиков. Они будут менять динамически.
• [e0, e1, ..., e8] - 9 коэффициентов полинома двигателя. Эти коэффициенты автомобиль должен будет отыскать/выучить. После окончания обучения они будут статичными.
• [w0, w1, ..., w8] - 9 коэффициентов полинома рулевого управления. Эти коэффициенты автомобиль должен будет отыскать/выучить. После окончания обучения они будут статичными.

Ценой использования более простой функции для мозга станет то, что автомобиль не сможет научиться некоторым сложным движениям, а также не сможет хорошо обобщать и хорошо адаптироваться к неизвестному окружению. Но для нашей конкретной стоянки и для демонстрации работы генетического алгоритма этого должно хватить.

Мы можем реализовать универсальную полиномиальную функцию следующим образом:

type Coefficients = number[];

// Calculates the value of a linear polynomial based on the coefficients and variables.
const linearPolynomial = (coefficients: Coefficients, variables: number[]): number => {
  if (coefficients.length !== (variables.length + 1)) {
    throw new Error('Incompatible number of polynomial coefficients and variables');
  }
  let result = 0;
  coefficients.forEach((coefficient: number, coefficientIndex: number) => {
    if (coefficientIndex < variables.length) {
      result += coefficient * variables[coefficientIndex];
    } else {
      // The last coefficient needs to be added up without multiplication.
      result += coefficient
    }
  });
  return result;
};

Мозг автомобиля в этом случае будет состоять из двух многочленов и будет выглядеть так:

const engineSignal: MuscleSignal = brainToMuscleSignal(
  linearPolynomial(engineCoefficients, sensors)
);

const wheelSignal: MuscleSignal = brainToMuscleSignal(
  linearPolynomial(wheelCoefficients, sensors)
);

Результатом функции linearPolynomial() является число с плавающей запятой. Функция brainToMuscleSignal() должна преобразовать широкий диапазон чисел с плавающей запятой в три конкретных целых числа, и она сделает это в два этапа:

1. Преобразует число с плавающей точкой широкого диапазона (например, 0.456 или 3673.45 или -280) в число с плавающей точкой ограниченного диапазона (0...1) (например, 0.05 или 0.86)
2. Преобразуйте число с плавающей запятой в диапазоне (0...1) в одно из трех целочисленных значений -1, 0, или +1. Например, числа с плавающей запятой, близкие к 0, будут преобразованы в -1, числа с плавающей запятой, близкие к 0.5, будут преобразованы в 0, а числа с плавающей запятой, близкие к +1, будут преобразованы в +1.

Чтобы выполнить первую часть преобразования, нам нужно ввести сигмоидную функцию, которая реализует следующую формулу:

https://trekhleb.dev/self-parking-car-evolution/article/images/05-sigmoid-01.svg

Сигмоид преобразует широкий диапазон чисел с плавающей запятой (ось x) в числа с плавающей запятой с ограниченным диапазоном (0...1) (ось y). Это именно то, что нам нужно.

Вот как шаги преобразования будут выглядеть на графике сигмоиды.

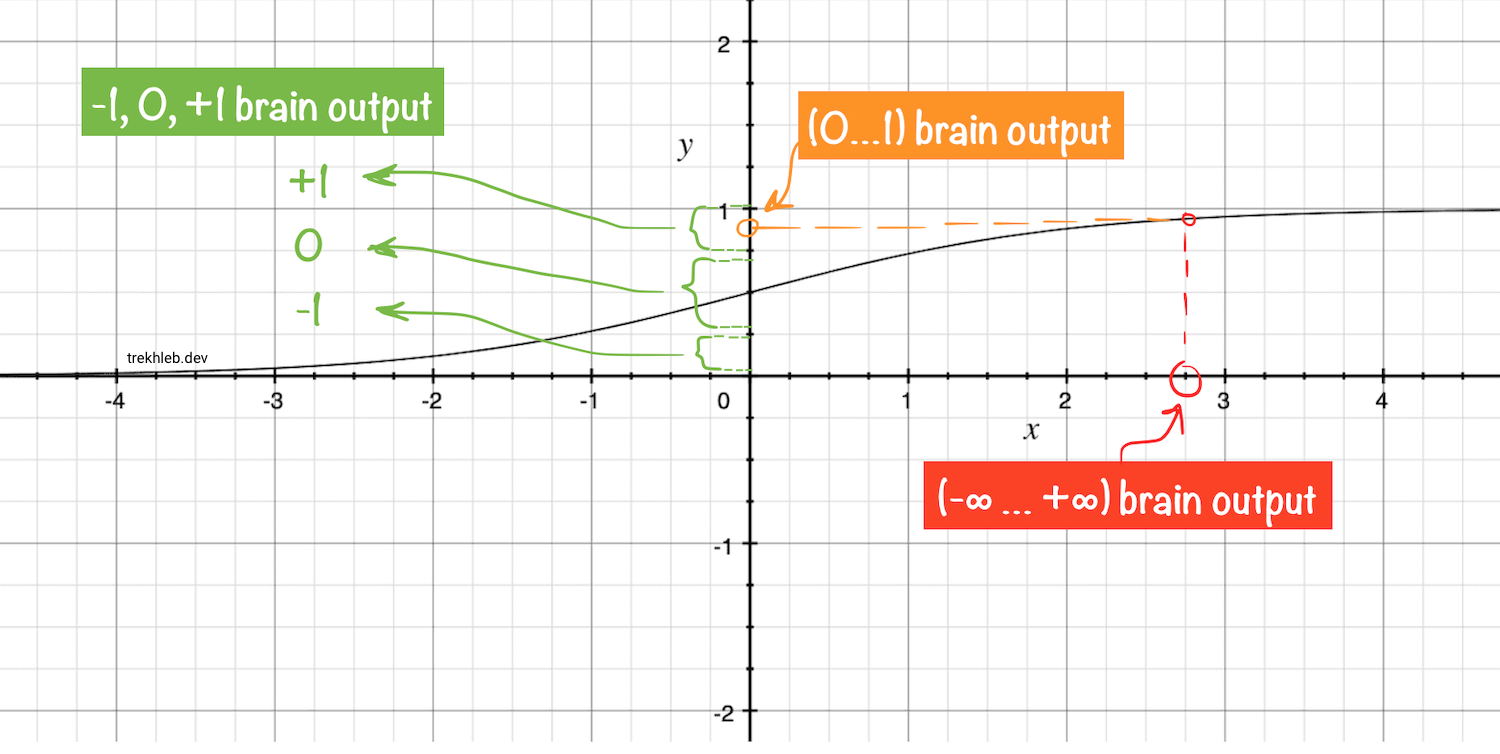
Реализация двух упомянутых выше шагов преобразования будет выглядеть так:

// Calculates the sigmoid value for a given number.
const sigmoid = (x: number): number => {
  return 1 / (1 + Math.E ** -x);
};

// Converts sigmoid value (0...1) to the muscle signals (-1, 0, +1)
// The margin parameter is a value between 0 and 0.5:
// [0 ... (0.5 - margin) ... 0.5 ... (0.5 + margin) ... 1]
const sigmoidToMuscleSignal = (sigmoidValue: number, margin: number = 0.4): MuscleSignal => {
  if (sigmoidValue < (0.5 - margin)) {
    return -1;
  }
  if (sigmoidValue > (0.5 + margin)) {
    return 1;
  }
  return 0;
};

// Converts raw brain signal to the muscle signal.
const brainToMuscleSignal = (rawBrainSignal: number): MuscleSignal => {
  const normalizedBrainSignal = sigmoid(rawBrainSignal);
  return sigmoidToMuscleSignal(normalizedBrainSignal);
}

Геном автомобиля (ДНК)

☝🏻 Главный вывод из разделов «Глаза», «Мышцы» и «Мозг» выше должен быть следующий - коэффициенты [e0, e1, ..., e8] и [w0, w1, ..., w8] определяют поведение машины. Эти 18 чисел вместе образуют уникальный геном автомобиля (или ДНК автомобиля).

Геном автомобиля в десятичной форме

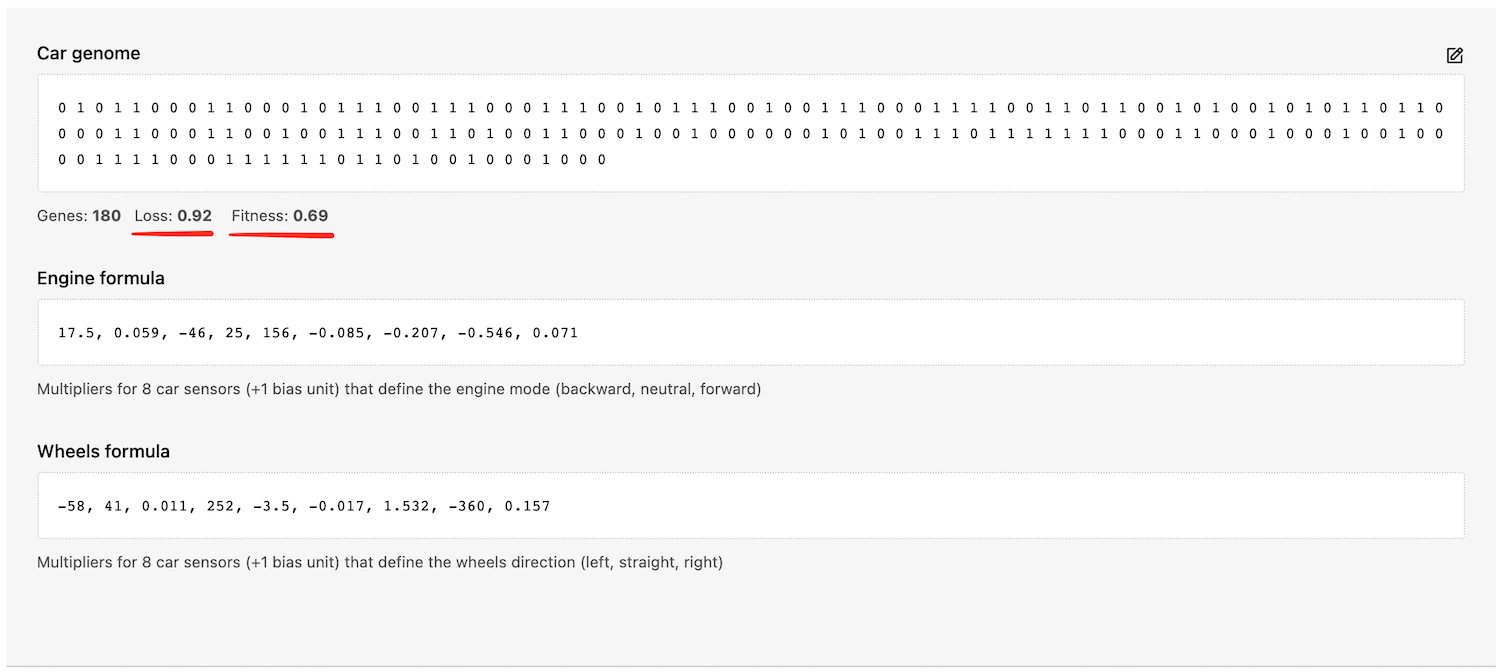
Соединим вместе коэффициенты мозга [e0, e1, ..., e8] и [w0, w1, ..., w8], чтобы сформировать геном автомобиля в десятичной форме:

// Car genome as a list of decimal numbers (coefficients).
const carGenomeBase10 = [e0, e1, ..., e8, w0, w1, ..., w8];

// i.e. carGenomeBase10 = [17.5, 0.059, -46, 25, 156, -0.085, -0.207, -0.546, 0.071, -58, 41, 0.011, 252, -3.5, -0.017, 1.532, -360, 0.157]

Геном автомобиля в двоичной форме

Давайте пойдем на шаг глубже (на уровень генов) и переведем десятичные числа генома автомобиля в двоичный формат (в простые единицы и нули).

Я подробно описал процесс преобразования чисел с плавающей запятой в двоичные числа в статье Binary representation of the floating-point numbers. Обратитесь к ней, если код в этом разделе непонятен.

Вот краткий пример того, как число с плавающей запятой может быть преобразовано в 16-битное двоичное число (опять же, можете обратиться к этой статье, если пример непонятен):

В нашем случае, чтобы уменьшить длину генома, мы преобразуем каждый плавающий коэффициент в нестандартное 10-битное двоичное число (1 знаковый бит, 4 бита экспоненты, 5 дробных битов).

Всего у нас 18 коэффициентов, каждый коэффициент будет преобразован в 10-битное число. Это означает, что геном автомобиля будет представлять собой массив нулей и единиц длиной 18 * 10 = 180 бит.

Например, для генома в десятичном формате, о котором говорилось выше, его двоичное представление будет выглядеть так:

type Gene = 0 | 1;

type Genome = Gene[];

const genome: Genome = [
  // Engine coefficients.
  0, 1, 0, 1, 1, 0, 0, 0, 1, 1, // <- 17.5
  0, 0, 0, 1, 0, 1, 1, 1, 0, 0, // <- 0.059
  1, 1, 1, 0, 0, 0, 1, 1, 1, 0, // <- -46
  0, 1, 0, 1, 1, 1, 0, 0, 1, 0, // <- 25
  0, 1, 1, 1, 0, 0, 0, 1, 1, 1, // <- 156
  1, 0, 0, 1, 1, 0, 1, 1, 0, 0, // <- -0.085
  1, 0, 1, 0, 0, 1, 0, 1, 0, 1, // <- -0.207
  1, 0, 1, 1, 0, 0, 0, 0, 1, 1, // <- -0.546
  0, 0, 0, 1, 1, 0, 0, 1, 0, 0, // <- 0.071

  // Wheels coefficients.
  1, 1, 1, 0, 0, 1, 1, 0, 1, 0, // <- -58
  0, 1, 1, 0, 0, 0, 1, 0, 0, 1, // <- 41
  0, 0, 0, 0, 0, 0, 1, 0, 1, 0, // <- 0.011
  0, 1, 1, 1, 0, 1, 1, 1, 1, 1, // <- 252
  1, 1, 0, 0, 0, 1, 1, 0, 0, 0, // <- -3.5
  1, 0, 0, 0, 1, 0, 0, 1, 0, 0, // <- -0.017
  0, 0, 1, 1, 1, 1, 0, 0, 0, 1, // <- 1.532
  1, 1, 1, 1, 1, 0, 1, 1, 0, 1, // <- -360
  0, 0, 1, 0, 0, 0, 1, 0, 0, 0, // <- 0.157
];

Только взгляните! Бинарный геном выглядит довольно зашифрованным. Но представьте себе, что эти 180 нулей и единиц определяют, как автомобиль ведет себя на стоянке! Это как если бы вы взломали чью-то ДНК и точно знаете, что означает каждый ген. Сильно!

Кстати, вы можете увидеть точные значения геномов и коэффициентов для наиболее "умного" автомобиля в панели симулятора

Вот исходный код, который выполняет преобразование из двоичного формата в десятичный формат чисел с плавающей запятой (мозгу он понадобится для декодирования генома и создания мышечных сигналов на основе данных генома):

type Bit = 0 | 1;

type Bits = Bit[];

type PrecisionConfig = {
  signBitsCount: number,
  exponentBitsCount: number,
  fractionBitsCount: number,
  totalBitsCount: number,
};

type PrecisionConfigs = {
  custom: PrecisionConfig,
};

const precisionConfigs: PrecisionConfigs = {
  // Custom-made 10-bits precision for faster evolution progress.
  custom: {
    signBitsCount: 1,
    exponentBitsCount: 4,
    fractionBitsCount: 5,
    totalBitsCount: 10,
  },
};

// Converts the binary representation of the floating-point number to decimal float number.
function bitsToFloat(bits: Bits, precisionConfig: PrecisionConfig): number {
  const { signBitsCount, exponentBitsCount } = precisionConfig;

  // Figuring out the sign.
  const sign = (-1) ** bits[0]; // -1^1 = -1, -1^0 = 1

  // Calculating the exponent value.
  const exponentBias = 2 ** (exponentBitsCount - 1) - 1;
  const exponentBits = bits.slice(signBitsCount, signBitsCount + exponentBitsCount);
  const exponentUnbiased = exponentBits.reduce(
    (exponentSoFar: number, currentBit: Bit, bitIndex: number) => {
      const bitPowerOfTwo = 2 ** (exponentBitsCount - bitIndex - 1);
      return exponentSoFar + currentBit * bitPowerOfTwo;
    },
    0,
  );
  const exponent = exponentUnbiased - exponentBias;

  // Calculating the fraction value.
  const fractionBits = bits.slice(signBitsCount + exponentBitsCount);
  const fraction = fractionBits.reduce(
    (fractionSoFar: number, currentBit: Bit, bitIndex: number) => {
      const bitPowerOfTwo = 2 ** -(bitIndex + 1);
      return fractionSoFar + currentBit * bitPowerOfTwo;
    },
    0,
  );

  // Putting all parts together to calculate the final number.
  return sign * (2 ** exponent) * (1 + fraction);
}

// Converts the 8-bit binary representation of the floating-point number to decimal float number.
function bitsToFloat10(bits: Bits): number {
  return bitsToFloat(bits, precisionConfigs.custom);
}

Мозговая функция, работающая с бинарным геномом

Раньше функция нашего мозга напрямую работала с десятичной формой полиномиальных коэффициентов engineCoefficients и wheelCoefficients. Однако теперь эти коэффициенты кодируются в двоичной форме генома. Давайте добавим функцию decodeGenome(), которая будет извлекать коэффициенты из генома, и перепишем мозговые функции следующим образом:

// Car has 16 distance sensors.
const CAR_SENSORS_NUM = 8;

// Additional formula coefficient that is not connected to a sensor.
const BIAS_UNITS = 1;

// How many genes do we need to encode each numeric parameter for the formulas.
const GENES_PER_NUMBER = precisionConfigs.custom.totalBitsCount;

// Based on 8 distance sensors we need to provide two formulas that would define car's behavior:
// 1. Engine formula (input: 8 sensors; output: -1 (backward), 0 (neutral), +1 (forward))
// 2. Wheels formula (input: 8 sensors; output: -1 (left), 0 (straight), +1 (right))
const ENGINE_FORMULA_GENES_NUM = (CAR_SENSORS_NUM + BIAS_UNITS) * GENES_PER_NUMBER;
const WHEELS_FORMULA_GENES_NUM = (CAR_SENSORS_NUM + BIAS_UNITS) * GENES_PER_NUMBER;

// The length of the binary genome of the car.
const GENOME_LENGTH = ENGINE_FORMULA_GENES_NUM + WHEELS_FORMULA_GENES_NUM;

type DecodedGenome = {
  engineFormulaCoefficients: Coefficients,
  wheelsFormulaCoefficients: Coefficients,
}

// Converts the genome from a binary form to the decimal form.
const genomeToNumbers = (genome: Genome, genesPerNumber: number): number[] => {
  if (genome.length % genesPerNumber !== 0) {
    throw new Error('Wrong number of genes in the numbers genome');
  }
  const numbers: number[] = [];
  for (let numberIndex = 0; numberIndex < genome.length; numberIndex += genesPerNumber) {
    const number: number = bitsToFloat10(genome.slice(numberIndex, numberIndex + genesPerNumber));
    numbers.push(number);
  }
  return numbers;
};

// Converts the genome from a binary form to the decimal form
// and splits the genome into two sets of coefficients (one set for each muscle).
const decodeGenome = (genome: Genome): DecodedGenome => {
  const engineGenes: Gene[] = genome.slice(0, ENGINE_FORMULA_GENES_NUM);
  const wheelsGenes: Gene[] = genome.slice(
    ENGINE_FORMULA_GENES_NUM,
    ENGINE_FORMULA_GENES_NUM + WHEELS_FORMULA_GENES_NUM,
  );

  const engineFormulaCoefficients: Coefficients = genomeToNumbers(engineGenes, GENES_PER_NUMBER);
  const wheelsFormulaCoefficients: Coefficients = genomeToNumbers(wheelsGenes, GENES_PER_NUMBER);

  return {
    engineFormulaCoefficients,
    wheelsFormulaCoefficients,
  };
};

// Update brain function for the engine muscle.
export const getEngineMuscleSignal = (genome: Genome, sensors: Sensors): MuscleSignal => {
  const {engineFormulaCoefficients: coefficients} = decodeGenome(genome);
  const rawBrainSignal = linearPolynomial(coefficients, sensors);
  return brainToMuscleSignal(rawBrainSignal);
};

// Update brain function for the wheels muscle.
export const getWheelsMuscleSignal = (genome: Genome, sensors: Sensors): MuscleSignal => {
  const {wheelsFormulaCoefficients: coefficients} = decodeGenome(genome);
  const rawBrainSignal = linearPolynomial(coefficients, sensors);
  return brainToMuscleSignal(rawBrainSignal);
};

Формулировка проблемы обучения автомобиля

☝🏻 Итак, наконец-то, мы подошли к моменту, когда высокоуровневая проблема обучения автомобиля самостоятельной парковке сводится к простой оптимизационной задаче поиска оптимальной комбинации 180 единиц и нулей (нахождение "достаточно хорошего" генома машины). Звучит просто, не правда ли?

Наивный подход

Мы могли бы подойти к проблеме поиска «достаточно хорошего» генома наивно и опробовать все возможные комбинации генов:

1. [0, ..., 0, 0], а затем ...
2. [0, ..., 0, 1], а затем ...
3. [0, ..., 1, 0], а затем ...
4. [0, ..., 1, 1], а затем ...
5. ...

Но давайте подсчитаем. Если у нас есть 180 бит и каждый бит равен либо 0 либо 1, у нас будет 2^180 (или 1.53 * 10^54) возможных комбинаций. Предположим, нам нужно дать 15 секунд на каждую машину, чтобы узнать, успешно она припаркуется или нет. Предположим также, что мы можем запустить симуляцию для 10 автомобилей одновременно. Тогда нам понадобится 15 * (1.53 * 10^54) / 10 = 2.29 * 10^54 [секунд], что составляет 7.36 * 10^46 [лет]. Довольно долгое придется ждать. Только сравните, что со дня рождения Иисуса Христа прошло только 2.021 * 10^3 [лет].

Генетический подход

Нам нужен более быстрый алгоритм, чтобы найти оптимальное значение генома. Здесь на помощь приходит генетический алгоритм. Возможно, мы и не найдем наилучшее значения генома, но есть шанс, что мы сможем найти оптимальное значение. И, что более важно, нам не нужно так долго ждать. С помощью симулятора эволюции я смог найти довольно хороший геном в течение 24 [часов].

Основы генетического алгоритма

Генетические алгоритмы вдохновлены процессом естественного отбора, обычно используются для решений оптимизационных задач. Они полагаются на биологически операторы, такие как кроссовер, мутация и отбор.

Проблема поиска «достаточно хорошей» комбинации генов для автомобиля выглядит как проблема оптимизации, так что есть большая вероятность, что генетический алгоритм поможет нам в этом.

Мы не будем подробно описывать генетический алгоритм, но в целом вот основные шаги, которые нам нужно будет сделать:

1. СОЗДАНИЕ - самое первое поколение автомобилей не может появиться из ничего, поэтому мы генерируем набор случайных геномов (набор двоичных массивов длиной 180). Например, мы можем создать ~1000 машин. Чем больше количество машин (население), тем выше шансы найти оптимальное решение (и найти его быстрее).
2. СЕЛЕКЦИЯ - нам нужно будет выбрать наиболее приспособленных особей из текущего поколения для дальнейшего спаривания (см. следующий шаг). Пригодность каждого индивидуума будет определяться на основе функции пригодности, которая в нашем случае покажет, насколько близко автомобиль приблизился к целевому месту парковки. Чем ближе машина к месту парковки, тем она "лучше".
3. СПАРИВАНИЕ - попросту говоря, мы позволим отобранным «♂ отцам- автомобилям» «заниматься сексом» с отобранными «♀ матерями-автомобилями», чтобы их геномы могли смешиваться в пропорции ~50/50 и производить «♂♀ детей-автомобилей». Идея состоит в том, что "рожденные" дети-автомобили могут стать лучше (или хуже) в парковке, если унаследуют лучшее (или худшее) у родителей.
4. МУТАЦИЯ - в процессе спаривания некоторые гены могут случайным образом мутировать (единицы и нули в геноме ребенка могут меняться). Это может привести к более широкому разнообразию геномов детей и, таким образом, к более широкому разнообразию поведения детей-автомобилей. Представьте, что 1-й бит был случайно установлен в 0 для всех ~1000 автомобилей. Единственный способ попробовать машину с 1-м битом, установленным в 1, - это случайные мутации. В то же время сильные мутации могут разрушить здоровые геномы.
5. Переходим к «Шагу №2», если количество поколений не достигло предела (например, не прошло 100 поколений) или пока самые успешные индивидуумы не достигли ожидаемого значения функции пригодности (например, если лучший автомобиль еще не приблизился к месту стоянки ближе, чем на 1 метр). В противном случае выходим из цикла.

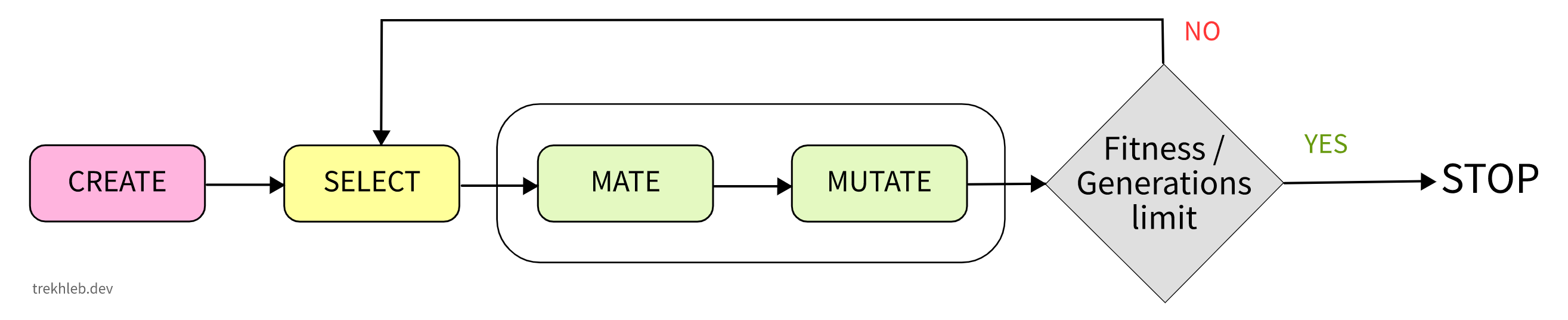
Развитие мозга автомобиля с помощью генетического алгоритма

Перед запуском генетического алгоритма давайте создадим функции для этапов «СОЗДАНИЯ», «СЕЛЕКЦИИ», «СПАРИВАНИЯ» и «МУТАЦИИ».

Функции для шага «СОЗДАНИЕ»

Функция createGeneration() создает массив случайных геномов ( популяцию или поколение) и принимает два параметра:

• generationSize - определяет размер поколения. Этот размер поколения будет неизменным в течение всего эволюционного процесса.
• genomeLength - определяет длину генома каждого индивидуума в популяции автомобилей. В нашем случае длина генома будет 180.

Вероятность того, что каждый ген генома будет равен 0 или 1, составляет 50/50.

type Generation = Genome[];

type GenerationParams = {
  generationSize: number,
  genomeLength: number,
};

function createGenome(length: number): Genome {
  return new Array(length)
    .fill(null)
    .map(() => (Math.random() < 0.5 ? 0 : 1));
}

function createGeneration(params: GenerationParams): Generation {
  const { generationSize, genomeLength } = params;
  return new Array(generationSize)
    .fill(null)
    .map(() => createGenome(genomeLength));
}

Функции для шага «МУТАЦИЯ»

Функция mutate() будет изменять некоторые гены случайным образом на основе значения mutationProbability.

Например, если mutationProbability = 0.1, то вероятность мутации каждого генома составляет 10% . Скажем, если бы у нас был геном длиной 10 генов, который выглядел бы как [0, 0, 0, 0, 0, 0 ,0 ,0 ,0 ,0], то после мутации будет вероятность, что 1 ген будет быть мутированным, и мы можем получить геном, который может выглядеть как [0, 0, 0, 1, 0, 0 ,0 ,0 ,0 ,0].

// The number between 0 and 1.
type Probability = number;

// @see: https://en.wikipedia.org/wiki/Mutation_(genetic_algorithm)
function mutate(genome: Genome, mutationProbability: Probability): Genome {
  for (let geneIndex = 0; geneIndex < genome.length; geneIndex += 1) {
    const gene: Gene = genome[geneIndex];
    const mutatedGene: Gene = gene === 0 ? 1 : 0;
    genome[geneIndex] = Math.random() < mutationProbability ? mutatedGene : gene;
  }
  return genome;
}

Функции для шага «СПАРИВАНИЕ»

Функция mate() примет геномы father и mother и произведет двух детей. Мы также произведем мутацию во время спаривания.

Каждый бит детского генома будет определяться на основе значений соответствующего бита генома отца или матери. Вероятность того, что ребенок унаследует бит отца или матери, составляет 50/50%. Например, предположим, что у нас есть геномы длиной 4 гена:

Father's genome: [0, 0, 1, 1]
Mother's genome: [0, 1, 0, 1]
                  ↓  ↓  ↓  ↓
Possible kid #1: [0, 1, 1, 1]
Possible kid #2: [0, 0, 1, 1]

В приведенном выше примере мутации не учитывались.

Реализация функции может выглядеть следующим образом:

// Performs Uniform Crossover: each bit is chosen from either parent with equal probability.
// @see: https://en.wikipedia.org/wiki/Crossover_(genetic_algorithm)
function mate(
  father: Genome,
  mother: Genome,
  mutationProbability: Probability,
): [Genome, Genome] {
  if (father.length !== mother.length) {
    throw new Error('Cannot mate different species');
  }

  const firstChild: Genome = [];
  const secondChild: Genome = [];

  // Conceive children.
  for (let geneIndex = 0; geneIndex < father.length; geneIndex += 1) {
    firstChild.push(
      Math.random() < 0.5 ? father[geneIndex] : mother[geneIndex]
    );
    secondChild.push(
      Math.random() < 0.5 ? father[geneIndex] : mother[geneIndex]
    );
  }

  return [
    mutate(firstChild, mutationProbability),
    mutate(secondChild, mutationProbability),
  ];
}

Функции для шага «СЕЛЕКЦИЯ»

Чтобы выбрать наиболее приспособленных особей для дальнейшего спаривания, нам нужен способ узнать пригодность каждого генома. Для этого воспользуемся так называемой фитнес-функцией.

Функция пригодности всегда связана с конкретной задачей, которую мы пытаемся решить, и не является универсальной. В нашем случае фитнес-функция будет измерять расстояние между автомобилем и местом парковки. Чем ближе машина к месту стоянки, тем она "лучше" (более пригодна). Мы реализуем фитнес-функцию чуть позже, а пока давайте опишем ее интерфейс:

type FitnessFunction = (genome: Genome) => number;

Теперь предположим, что у нас есть значения пригодности для каждого индивидуума популяции. Предположим также, что мы отсортировали всех индивидуумов по их значениям приспособленности, так что первые особи являются самыми сильными. Как выбрать отцов и матерей из этого массива? Нам необходимо произвести отбор таким образом, чтобы чем выше значение приспособленности индивидуума, тем выше шансы, что этот индивидуум будет выбран для спаривания. В этом нам поможет функция weightedRandom().

// Picks the random item based on its weight.
// The items with a higher weight will be picked more often.
const weightedRandom = <T>(items: T[], weights: number[]): { item: T, index: number } => {
  if (items.length !== weights.length) {
    throw new Error('Items and weights must be of the same size');
  }

  // Preparing the cumulative weights array.
  // For example:
  // - weights = [1, 4, 3]
  // - cumulativeWeights = [1, 5, 8]
  const cumulativeWeights: number[] = [];
  for (let i = 0; i < weights.length; i += 1) {
    cumulativeWeights[i] = weights[i] + (cumulativeWeights[i - 1] || 0);
  }

  // Getting the random number in a range [0...sum(weights)]
  // For example:
  // - weights = [1, 4, 3]
  // - maxCumulativeWeight = 8
  // - range for the random number is [0...8]
  const maxCumulativeWeight = cumulativeWeights[cumulativeWeights.length - 1];
  const randomNumber = maxCumulativeWeight * Math.random();

  // Picking the random item based on its weight.
  // The items with higher weight will be picked more often.
  for (let i = 0; i < items.length; i += 1) {
    if (cumulativeWeights[i] >= randomNumber) {
      return {
        item: items[i],
        index: i,
      };
    }
  }
  return {
    item: items[items.length - 1],
    index: items.length - 1,
  };
};

Использовать эту функцию довольно просто. Допустим, вы очень любите бананы и хотите есть их чаще, чем клубнику. Вы можете вызвать функцию const fruit = weightedRandom(['banana', 'strawberry'], [9, 1]), и в ≈9 случаях из 10 переменная fruit будет равна banana, и только в ≈1 из 10 случаев она будет равна strawberry.

Чтобы избежать потери лучших особей (назовем их чемпионами) в процессе спаривания, мы можем также ввести так называемый параметр longLivingChampionsPercentage. Например, если longLivingChampionsPercentage = 10, то 10% лучших автомобилей из предыдущей популяции будут перенесены в новое поколение. Вы можете представить, что есть некоторые долгожители, которые могут прожить долгую жизнь и увидеть своих детей и даже внуков.

Мы можем реализовать функцию select() следующим образом:

// The number between 0 and 100.
type Percentage = number;

type SelectionOptions = {
  mutationProbability: Probability,
  longLivingChampionsPercentage: Percentage,
};

// @see: https://en.wikipedia.org/wiki/Selection_(genetic_algorithm)
function select(
  generation: Generation,
  fitness: FitnessFunction,
  options: SelectionOptions,
) {
  const {
    mutationProbability,
    longLivingChampionsPercentage,
  } = options;

  const newGeneration: Generation = [];

  const oldGeneration = [...generation];
  // First one - the fittest one.
  oldGeneration.sort((genomeA: Genome, genomeB: Genome): number => {
    const fitnessA = fitness(genomeA);
    const fitnessB = fitness(genomeB);
    if (fitnessA < fitnessB) {
      return 1;
    }
    if (fitnessA > fitnessB) {
      return -1;
    }
    return 0;
  });

  // Let long-liver champions continue living in the new generation.
  const longLiversCount = Math.floor(longLivingChampionsPercentage * oldGeneration.length / 100);
  if (longLiversCount) {
    oldGeneration.slice(0, longLiversCount).forEach((longLivingGenome: Genome) => {
      newGeneration.push(longLivingGenome);
    });
  }

  // Get the data about he fitness of each individuum.
  const fitnessPerOldGenome: number[] = oldGeneration.map((genome: Genome) => fitness(genome));

  // Populate the next generation until it becomes the same size as a old generation.
  while (newGeneration.length < generation.length) {
    // Select random father and mother from the population.
    // The fittest individuums have higher chances to be selected.
    let father: Genome | null = null;
    let fatherGenomeIndex: number | null = null;
    let mother: Genome | null = null;
    let matherGenomeIndex: number | null = null;

    // To produce children the father and mother need each other.
    // It must be two different individuums.
    while (!father || !mother || fatherGenomeIndex === matherGenomeIndex) {
      const {
        item: randomFather,
        index: randomFatherGenomeIndex,
      } = weightedRandom<Genome>(generation, fitnessPerOldGenome);

      const {
        item: randomMother,
        index: randomMotherGenomeIndex,
      } = weightedRandom<Genome>(generation, fitnessPerOldGenome);

      father = randomFather;
      fatherGenomeIndex = randomFatherGenomeIndex;

      mother = randomMother;
      matherGenomeIndex = randomMotherGenomeIndex;
    }

    // Let father and mother produce two children.
    const [firstChild, secondChild] = mate(father, mother, mutationProbability);

    newGeneration.push(firstChild);

    // Depending on the number of long-living champions it is possible that
    // there will be the place for only one child, sorry.
    if (newGeneration.length < generation.length) {
      newGeneration.push(secondChild);
    }
  }

  return newGeneration;
}

Фитнеса-функция (функция пригодности)

Пригодность автомобиля будет определяться расстоянием от автомобиля до места парковки. Чем выше дистанция, тем ниже пригодность.

Мы будем рассчитывать среднее расстояние от 4 колес автомобиля до соответствующих 4 углов парковочного места. Это расстояние мы будем называть потерей (уроном), которая обратно пропорциональна приспособленности.

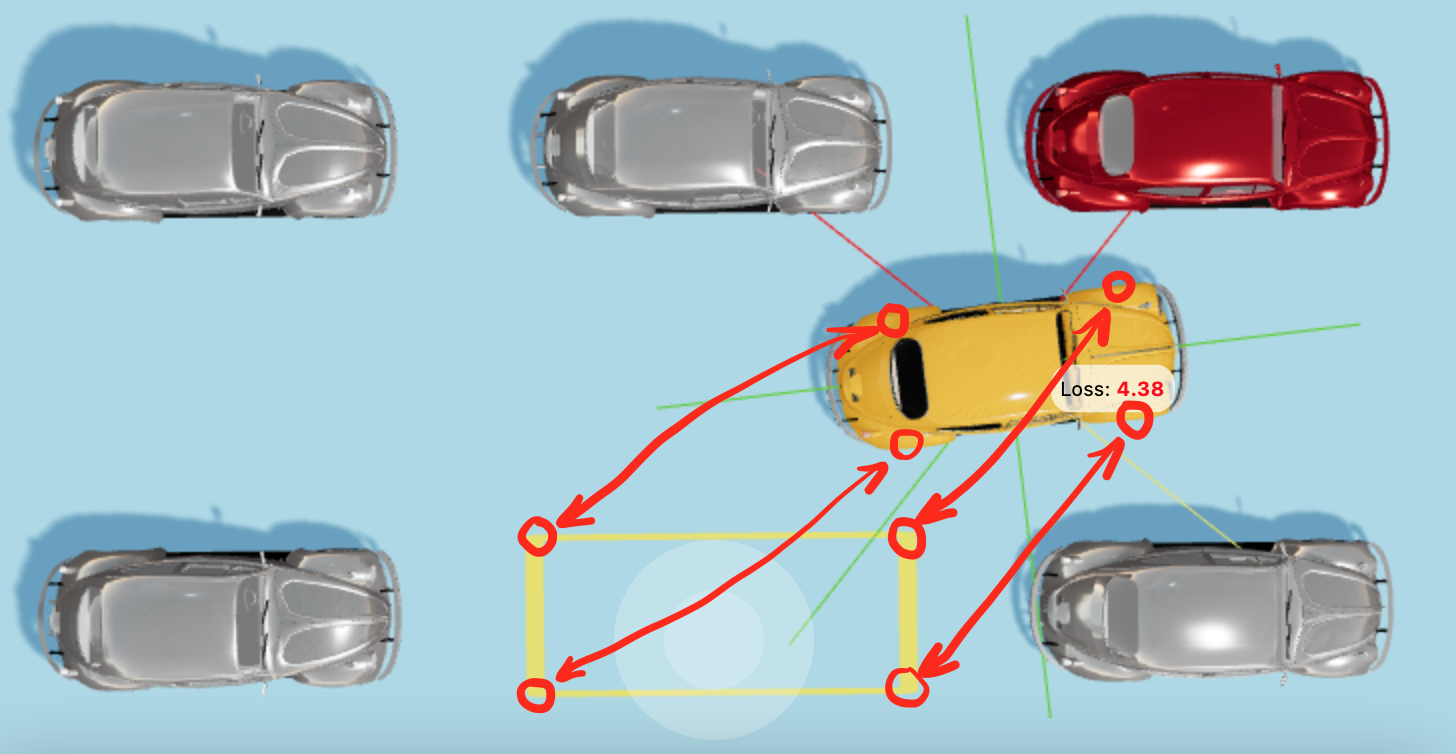
Вычисление расстояния между каждым колесом и каждым углом по отдельности (вместо простого расчета расстояния от центра автомобиля до центра парковочного места) позволит автомобилю сохранять правильную ориентацию относительно парковочного места.

Расстояние между двумя точками в пространстве будет вычисляться на основе теоремы Пифагора (ура! она наконец-то понадобилась после школы!) следующим образом:

type NumVec3 = [number, number, number];

// Calculates the XZ distance between two points in space.
// The vertical Y distance is not being taken into account.
const euclideanDistance = (from: NumVec3, to: NumVec3) => {
  const fromX = from[0];
  const fromZ = from[2];
  const toX = to[0];
  const toZ = to[2];
  return Math.sqrt((fromX - toX) ** 2 + (fromZ - toZ) ** 2);
};

Расстояние между автомобилем и местом парковки (урон) будет рассчитываться следующим образом:

type RectanglePoints = {
  fl: NumVec3, // Front-left
  fr: NumVec3, // Front-right
  bl: NumVec3, // Back-left
  br: NumVec3, // Back-right
};

type GeometricParams = {
  wheelsPosition: RectanglePoints,
  parkingLotCorners: RectanglePoints,
};

const carLoss = (params: GeometricParams): number => {
  const { wheelsPosition, parkingLotCorners } = params;

  const {
    fl: flWheel,
    fr: frWheel,
    br: brWheel,
    bl: blWheel,
  } = wheelsPosition;

  const {
    fl: flCorner,
    fr: frCorner,
    br: brCorner,
    bl: blCorner,
  } = parkingLotCorners;

  const flDistance = euclideanDistance(flWheel, flCorner);
  const frDistance = euclideanDistance(frWheel, frCorner);
  const brDistance = euclideanDistance(brWheel, brCorner);
  const blDistance = euclideanDistance(blWheel, blCorner);

  return (flDistance + frDistance + brDistance + blDistance) / 4;
};

Поскольку пригодность (fitness) должна быть обратно пропорциональна урону (loss), мы рассчитаем ее следующим образом:

const carFitness = (params: GeometricParams): number => {
  const loss = carLoss(params);
  // Adding +1 to avoid a division by zero.
  return 1 / (loss + 1);
};

Вы можете увидеть значения fitness и loss для определенного генома и для текущего положения автомобиля на панели симулятора:

Запускаем эволюцию

Соберем вместе функции эволюции. Мы собираемся «создать мир», запустить цикл эволюции, заставить время идти, поколение - эволюционировать, а автомобили - учиться парковаться.

Чтобы получить значения пригодности для каждой машины, нам нужно запустить симуляцию поведения машин в виртуальном трехмерном мире. Симулятор эволюции делает именно это - он запускает приведенный ниже код в симуляторе, созданном с помощью Three.js:

// Evolution setup example.
// Configurable via the Evolution Simulator.
const GENERATION_SIZE = 1000;
const LONG_LIVING_CHAMPIONS_PERCENTAGE = 6;
const MUTATION_PROBABILITY = 0.04;
const MAX_GENERATIONS_NUM = 40;

// Fitness function.
// It is like an annual doctor's checkup for the cars.
const carFitnessFunction = (genome: Genome): number => {
  // The evolution simulator calculates and stores the fitness values for each car in the fitnessValues map.
  // Here we will just fetch the pre-calculated fitness value for the car in current generation.
  const genomeKey = genome.join('');
  return fitnessValues[genomeKey];
};

// Creating the "world" with the very first cars generation.
let generationIndex = 0;
let generation: Generation = createGeneration({
  generationSize: GENERATION_SIZE,
  genomeLength: GENOME_LENGTH, // <- 180 genes
});

// Starting the "time".
while(generationIndex < MAX_GENERATIONS_NUM) {
  // SIMULATION IS NEEDED HERE to pre-calculate the fitness values.

  // Selecting, mating, and mutating the current generation.
  generation = select(
    generation,
    carFitnessFunction,
    {
      mutationProbability: MUTATION_PROBABILITY,
      longLivingChampionsPercentage: LONG_LIVING_CHAMPIONS_PERCENTAGE,
    },
  );

  // Make the "time" go by.
  generationIndex += 1;
}

// Here we may check the fittest individuum of the latest generation.
const fittestCar = generation[0];

После запуска функции select() массив generation сортируется по значениям пригодности в порядке убывания. Следовательно, наиболее приспособленный автомобиль всегда будет первым автомобилем в массиве.

Автомобили 1-го поколения со случайным геномом будут вести себя примерно так:

Автомобили ≈40-го поколения начинают учиться парковаться самостоятельно и все ближе приближаются к месту парковки:

Другой пример с немного более сложной стартовой точкой:

По пути машины сталкиваются с другими машинами, а также неточно занимают парковочное место, но это всего-лишь 40-е поколение с момента создания мира для них, так что вы можете дать машинам еще немного времени для обучения.

Из поколения в поколение мы можем видеть, как урон уменьшается (что означает, что значения пригодности растут). P50 Avg Loss показывает среднее значение урона (среднее расстояние от автомобилей до места парковки) для 50% наиболее приспособленных автомобилей. Min Loss показывает урон наиболее приспособленного автомобиля в каждом поколении.

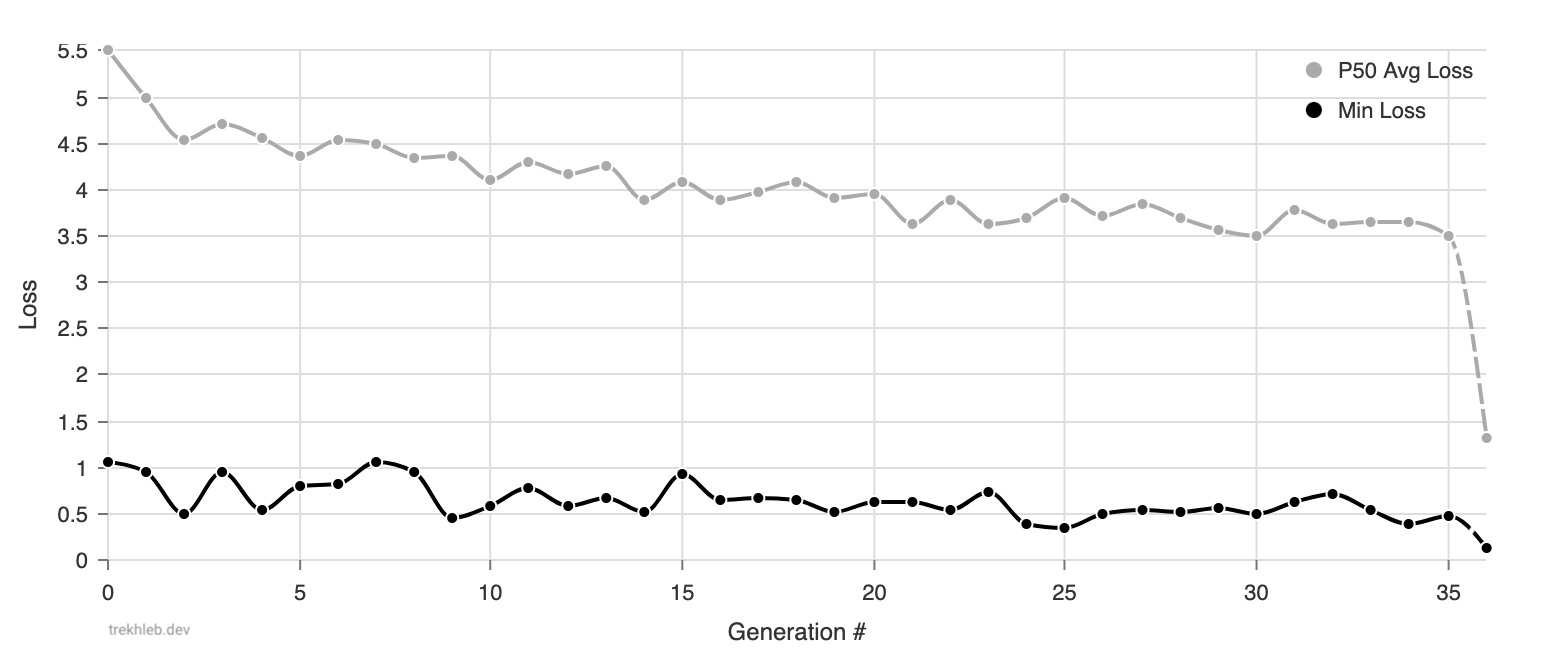
Вы можете видеть, что в среднем 50% наиболее приспособленных автомобилей учатся приближаться к месту парковки (от 5,5м от места парковки до 3,5м за 35 поколений). Тренд для значений Min Loss менее очевиден (от 1м до 0,5м с некоторыми шумом), однако из анимации выше вы можете увидеть, что автомобили научились некоторым базовым парковочным движениям.

Заключение

В этой статье мы свели высокоуровневую задачу создания авто способного парковаться самостоятельно к более простой и низкоуровневой задаче нахождения оптимальной комбинации из 180 единиц и нулей (нахождение оптимального генома автомобиля).

Затем мы применили генетический алгоритм, чтобы найти оптимальный геном автомобиля. Это позволило нам получить довольно хорошие результаты за несколько часов моделирования (вместо потенциальных многих лет использования наивного подхода).

Вы можете запустить 🚕 Симулятор эволюции, чтобы увидеть эволюционный процесс прямо в браузере. Симулятор предоставляет следующие возможности:

• Вы сможете начать тренировку машин с нуля и изменить параметры эволюции
• Вы сможете увидеть как паркуются уже натренированные авто
• Вы также можете попробовать припарковать авто вручную

Полный генетический исходный код, показанный в этой статье, также можно найти в репозитории Evolution Simulator repository. Если вы один из тех, кто действительно будет считать и проверять количество строк, чтобы убедиться, что их меньше 500 (без учета тестов), пожалуйста, проверьте код здесь 🥸.

Остался еще ряд нерешенных проблем с кодом и симулятором:

• Мозг автомобиля слишком упрощен и использует линейные уравнения вместо, скажем, нейронных сетей. Это делает автомобиль неприспособленным к новому окружению или новым типам парковок.
• Мы не уменьшаем значение пригодности машины, когда она наезжает на другую машину. Таким образом, автомобиль не «чувствует» никакой вины в создании ДТП.
• Симулятор эволюции нестабилен. Это означает, что один и тот же автомобильный геном может давать немного разные значения приспособленности, что делает эволюцию менее эффективной.
• Симулятор эволюции также очень "тяжелый" с точки зрения производительности, что замедляет прогресс эволюции, поскольку мы не можем обучить, скажем, 1000 машин одновременно.
• Также симулятор требует, чтобы вкладка браузера была открыта и активна для выполнения симуляции.
• и пр.

Тем не менее, целью этой статьи было изучение того, как работает генетический алгоритм, а не создание самопаркующейся Tesla. Я надеюсь, вы хорошо провели время, читая статью, даже с учетом упомянутых выше недоработок.