Думаю, в клубе есть много ребят, которые любят решать математические головоломки и задачки. Предлагаю в этом треде собрать ваши самые любимые задачки.
На первом уровне комментариев пишем условие задачки (без решения). А вот как лучше публиковать решение не знаю. Идеально было бы скрывать решение за спойлером. Но не нашёл такой функции в маркдаун. Поэтому, думаю, за решением лучше стучаться в личку к автору комментария с задачкой. Если есть другой способ, предлагайте.

Условие задачи
Вот недавно попалась такая задачка.
Есть тёмная комната. В комнате стоит стол. На столе в случайном порядке лежат 100 монет. 88 монет лежит орлом вверх, 12 решкой вверх. Вам надо зайти в комнату и разделить монеты на две кучи (необязательно одинаковые). В каждой куче должно быть одинаковое количество решек. На ощупь определить орёл или решка нельзя.
Я сам пока не решил.
😱 Комментарий удален его автором...
В левой части написано х в степени х, который в степени х и т.д. счётное число раз. Нужно найти х. После этого предлагается решить также следующее уравнение: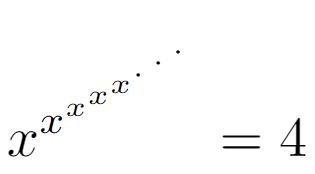
В последнее время подсел на числовые ребусы. Они достаточно простые и не напрягают мозг, поэтому скорее релаксируешь в процессе. Очень нравится на айпаде черкать, прямо наслаждаюсь)
**Каждую букву необходимо заменить на цифру. При этом, каждая цифра может встречаться один раз. Т.е. если буква А=1, то буква Г уже не может быть единицей. **
Условие задачи
Детская задачка:
Рыба весит 8 килограмм плюс половина ее собственного веса, сколько весит рыба?
А может решения прям в комментах писать? Обсуждение живое будет, ну и не с первого раза ответы правильные будут, наверное :)
Условие задачи
Есть 12 монет. Одна из них фальшивая. При этом неизвестно, больше весит фальшивая монета или меньше. Нужно найти фальшивую монетку с помощью только 3 взвешиваний весов.
Условие задачи
Адаптируем задачу под IT специфику:
Есть 2 проекта, один гарантиовано провальный, другой простой и понятный. Есть 2 заказчика, по одному на проект. Оба заказчика знают правду про проекты и друг про друга. Один патологический лжец, а другой всегда говорит правду, но вы не знаете кто есть кто. Вы можете задать 1 вопрос одному из заказчиков и на основе единственного ответа выбрать проект. Сформулируйте свой вопрос и стратегию выбора.
Я когда-то залипал на этом сайте https://braingames.ru/, очень рекомендую. Куча классных задач по математике/логике и прочему
Предлагаю порешать задачи с маткружка, который я заканчивал: http://mathcenter.spb.ru/12/series/index.html . Рекомендую начинать с пятого класса (в самом низу) и идти по сериям.
Например, вот моя любимая, первая серия первого летнего лагеря:
Условие задачи
Имеется 13 серых, 15 бурых и 17 малиновых хамелеонов. Сталкиваясь, два разноцветных хамелеона перекрашиваются в третий цвет (например, из серого и бурого хамелеонов образуется два малиновых). Докажите, что все хамелеоны никогда не приобретут один и тот же цвет.
На плоскости накидано какое-то конечное количество точек, причем никакие три не находятся на одной прямой. Через одну из них — P — проведена прямая так, что она не содержит никакие другие точки. Назовем «мельницей графа Дуку» такой процесс, при котором мы поворачиваем эту прямую по часовой вокруг этой точки, пока она не зацепит какую-то новую точку Q, после чего она продолжает вращаться по часовой вокруг Q, пока не зацепит R, и так далее.
Докажите, что при любом заранее заданном числе и расположении точек можно выбрать начальное расположение прямой так, чтобы она своей «мельницей» прошлась по всем точкам бесконечное число раз (за бесконечное время)